Shock polar
The term shock polar is generally used with the graphical representation of the Rankine-Hugoniot equations in either the hodograph plane or the pressure ratio-flow deflection angle plane. The polar itself is the locus of all possible states after an oblique shock.
Shock Polar in the 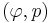 Plane
Plane
The minimum angle,  , which an oblique shock can have is the Mach angle
, which an oblique shock can have is the Mach angle 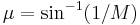 , where
, where  is the initial Mach number before the shock and the greatest angle corresponds to a normal shock. The range of shock angles is therefore
is the initial Mach number before the shock and the greatest angle corresponds to a normal shock. The range of shock angles is therefore 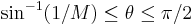 . To calculate the pressures for this range of angles,the Rankine-Hugoniot equations are solved for pressure:
. To calculate the pressures for this range of angles,the Rankine-Hugoniot equations are solved for pressure:
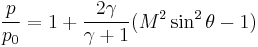
To calculate the possible flow deflection angles, the relationship between shock angle  and
and  is used:
is used:
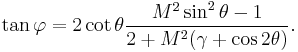
Where  is the ratio of specific heats and
is the ratio of specific heats and  is the flow deflection angle.
is the flow deflection angle.
Uses of Shock Polars
One of the primary uses of shock polars is in the field of shock wave reflection. A shock polar is plotted for the conditions before the incident shock, and a second shock polar is plotted for the conditions behind the shock, with its origin located on the first polar, at the angle through which the incident shock wave deflects the flow. Based on the intersections between the incident shock polar and the reflected shock polar, conclusions as to which reflection patterns are possible may be drawn. Often, it is used to graphically determine whether regular shock reflection is possible, or whether Mach reflection occurs.[1][2]
References
- Chapman, C.J. (2000). High Speed Flow. CUP. ISBN 978-0521661690.
- Anderson, John D. Jr. (January 2001) [1984]. Fundamentals of Aerodynamics (3rd Edition ed.). McGraw-Hill Science/Engineering/Math. ISBN 0-07-237335-0.
- ^ Ben-Dor, Gabi (2007). Shock Wave Reflection Phenomena (2nd Edition ed.). Springer. ISBN 978-3-540-71381-4.
- ^ "Transition between Regular Reflection and Mach Reflection in the Dual-Solution Domain" (PDF). 2007. http://thesis.library.caltech.edu/36/1/ThesisRootFinal.pdf. Retrieved 2010-08-13.